সূত্র ১। $(a+b{)}^2=a^2+2ab+b^2$

প্রমাণ:

$(a+b{)}^2$ এর অর্থ (a + b) কে (a + b) দ্বারা গুণ।

$(a+b{)}^2=(a+b\left)\right(a+b)$

= a(a + b) + b(a + b) [বহুপদী রাশিকে বহুপদী রাশি দ্বারা গুণ]

$=a^2+ab+ba+b^2$

$=a^2+ab+ab+b^2$

$(a+b{)}^2=a^2+2ab+b^2$

সূত্রটির জ্যামিতিক ব্যাখ্যা

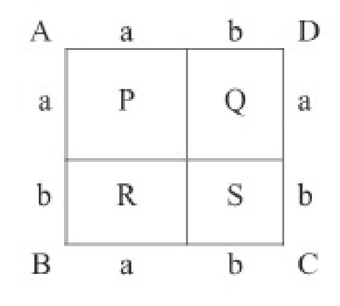
ABCD একটি বর্গক্ষেত্র যার

AB বাহু = a + b
BC বাহু = a+b

ABCD বর্গক্ষেত্রের ক্ষেত্রফল = (বাহুর দৈর্ঘ্য)^২

= (a + b)^২

বর্গক্ষেত্রটিকে P.Q, R, S চারটি ভাগে ভাগ করা হয়েছে।

এখানে P ও S বর্গক্ষেত্র এবং Q ও R আয়তক্ষেত্র।

আমরা জানি, বর্গক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য)² এবং আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য $\times$ প্রস্থ

অতএব,

P এর ক্ষেত্রফল = $a\times a=a^2$

Q এর ক্ষেত্রফল = $a\times b = ab$

R এর ক্ষেত্রফল = $a\times b = ab$

S এর ক্ষেত্রফল = $b\times b=b^2$

এখন, ABCD বর্গক্ষেত্রের ক্ষেত্রফল = (P+Q+R+S) এর ক্ষেত্রফল

$(a+b{)}^2=a^2+ab+ab+b^2$

$=a^2+2ab+b^2$

$\therefore$ $(a+b{)}^2=a^2+2ab+b^2$

অনুসিদ্ধান্ত ১। $a^2+b^2=(a+b{)}^2-2ab$

আমরা জানি, $(a+b{)}^2=a^2+2ab+b^2$

বা, $(a+b{)}^2-2ab=a^2+2ab+b^2-2ab$ [উভয়পক্ষ থেকে 2ab বিয়োগ করে]

বা, $(a+b{)}^2-2ab=a^2+b^2$

$\therefore$ $a^2+b^2=(a+b{)}^2-2ab$

উদাহরণ ১। (m + n) এর বর্গ নির্ণয় কর।

সমাধান:

(m + n) এর বর্গ = $(m+n{)}^2$

$=(m{)}^2+2mn+(n{)}^2$

$=m^2+2mn+n^2$

উদাহরণ ২। (3x + 4) এর বর্গ নির্ণয় কর।

সমাধান:

(3x + 4) এর বর্গ = $(3x+4{)}^2$

$=(3x{)}^2+2\times 3x\times 4+(4{)}^2$

$=9x^2+24x+16$

উদাহরণ ৩। (2x + 3y) এর বর্গ নির্ণয় কর।

সমাধান:

(2x + 3y) এর বর্গ = $(2x+3y{)}^2$

$=(2x{)}^2+2\times 2x\times 3y+(3y{)}^2$

$=4x^2+12xy+9y^2$

উদাহরণ ৪। বর্গের সূত্র প্রয়োগ করে 105 এর বর্গ নির্ণয় কর।

সমাধান:

$(105{)}^2=(100+5{)}^2$

$=(100{)}^2+2\times 100\times 5+(5{)}^2$

= 10000+1000+25

= 11025

সূত্র ২। $(a-b{)}^2=a^2-2ab+b^2$

${(a-b)}^2$ এর অর্থ (a-b) কে (a-b) দ্বারা গুণ।

$\therefore$ $(a-b{)}^2=(a-b\left)\right(a-b)$

=a(a-b)-b(a-b)

$= a^2-ab-ba + b^2$

$= a^2-ab-ab+b^2$

$\therefore$ $(a-b{)}^2=a^2-2ab+b^2$

লক্ষ করি: দ্বিতীয় সূত্রটি প্রথম সূত্রের সাহায্যেও নির্ণয় করা যায়।

আমরা জানি,

$(a+b{)}^2=a^2+2ab+b^2$

এখন

$(a-b{)}^2= (a+(-b){ }^2=a^2+2a(-b)+(-b{)}^2$ [b এর পরিবর্তে - b বসিয়ে ]

$=a^2-2ab+b^2$

অনুসিদ্ধান্ত ২। $a^2+b^2=(a-b{)}^2+2ab$

আমরা জানি, $(a-b{)}^2=a^2-2ab+b^2$

বা, $(a-b{)}^2+2ab=a^2-2ab+b^2+2ab$

বা, $(a-b{)}^2+2ab=a^2+b^2$

$\therefore$ $a^2+b^2=(a-b{)}^2+2ab$

উদাহরণ ৫। p - q এর বর্গ নির্ণয় কর।

সমাধান:

(p + q) এর বর্গ = $(p-q{)}^2$

$=(p{)}^2-2pq+(q{)}^2$

$=p^2-2pq+q^2$

উদাহরণ ৬। (5x - 3y) এর বর্গ নির্ণয় কর।

সমাধান:

(5x + 3y) এর বর্গ = $(5x-3y{)}^2$

$=(5x{)}^2-2\times 5x\times 3y+(3y{)}^2$

$=25x^2-30xy+9y^2$

উদাহরণ ৭। বর্গের সূত্র প্রয়োগ করে 98 এর বর্গ নির্ণয় কর।

সমাধান:

$(98{)}^2=(100-2{)}^2$

$=(100{)}^2-2\times 100\times 2+(2{)}^2$

=10000-400+4

= 9604

প্রথম ও দ্বিতীয় সুত্রের আরও কয়েকটি অনুসিদ্ধান্ত:

অনুসিদ্ধান্ত ৩।

$(a+b{)}^2=a^2+2ab+b^2$

$=a^2+b^2-2ab+4ab$ $[ \because + 2ab = - 2ab + 4ab ]$

$=a^2-2ab+b^2+4ab$

$=(a-b{)}^2+4ab$

$\therefore$ $(a+b{)}^2=(a-b{)}^2+4ab$

অনুসিদ্ধান্ত ৪।

$(a-b{)}^2=a^2-2ab+b^2$

$=a^2+b^2+2ab-4ab$

$=a^2+2ab+b^2-4ab$

$=(a-b{)}^2-4ab$

$\therefore$$(a-b{)}^2=(a+b{)}^2-4ab$

অনুসিদ্ধান্ত ৫।

$(a+b{)}^2+(a-b{)}^2=(a^2+2ab+b^2)+(a^2-2ab+b^2)$

$=a^2+2ab+b^2+a^2-2ab+b^2$

$=2a^2+2b^2$

$=2(a^2+b^2)$

$\therefore$$(a+b{)}^2+(a-b{)}^2=2(a^2+b^2)$

অনুসিদ্ধান্ত ৬।

$(a+b{)}^2-(a-b{)}^2=(a^2+2ab+b^2)-(a^2-2ab+b^2)$

$=a^2+2ab+b^2-a^2+2ab-b^2$

= 4ab

$\therefore$ $(a+b{)}^2-(a-b{)}^2=4ab$

উদাহরণ ৮। a + b = 7 এবং ab = 9 হলে, a² + b² এর মান নির্ণয় কর।

সমাধান:

আমরা জানি,

$a^2+b^2=(a+b{)}^2-2ab$

$= {\left(7\right)}^2-2x9$

=49-18

=31

উদাহরণ ৯। a + b = 5 এবং ab = 6 হলে, (a-b)² এর মান নির্ণয় কর।

সমাধান:

আমরা জানি,

$(a-b{)}^2=(a+b{)}^2-4ab$

$= {\left(5\right)}^2-4x6$

=25-24

=1

উদাহরণ ১০। $p-\frac{1}{p}=8$ হলে, প্রমাণ কর যে $p^2+\frac{1}{p^2}=66$

সমাধান:

$p^2+\frac{1}{p^2}= {\left(p-\frac{1}{p}\right)}^2+2\times p\times \frac{1}{p}$ $[\because a^2+b^2=(a-b{)}^2+2ab]$

$=(8{)}^2+2$

= 64+2

= 66 (প্রমাণিত)

উদাহরণ ১১। a + b + c এর বর্গ নির্ণয় কর।

সমাধান:

ধরি, a + b = p

$\therefore$ $(a+b+c{)}^2$

$=\left\{\right(a+b)+c{\}}^2$

$=(p+c{)}^2$

$=p^2+2pc+c^2$

$=(a+b{)}^2+2(a+b)c+c^2$

$=a^2+2ab+b^2+2ac+2bc+c^2$

$=a^2+b^2+c^2+2ab+2bc+2ca$

উদাহরণ ১২। (x + y - z) এর বর্গ নির্ণয় কর।

সমাধান:

ধরি, x + y = m

$\therefore (x+y-z{)}^2= \left\{x+y)-z{ }^2\right\}$

$=(m-z{)}^2$

$=m^2-2mz+z^2$

$=(x+y{)}^2-2x(x+y)z+z^2$ [m-এর মান বসিয়ে]

$=x^2+2xy+y^2-2xz-2yz+z^2$

$=x^2+y^2+z^2+2xy-2xz-2yz$

উদাহরণ ১৩। 3x - 2y + 5z এর বর্গ নির্ণয় কর।

সমাধান:

3x - 2y + 5z এর বর্গ

$=\left\{\right(3x-2y)+5z{\}}^2$

$=(3x-2y{)}^2+2(3x-2y)5z+(5z{)}^2$

$=(3x{)}^2-2\times 3x\times 2y+(2y{)}^2+2\times 5z(3x-2y)+25z^2$

$=9x^2-12xy+4y^2+30xz-20yz+25z^2$

$=9x^2+4y^2+25z^2-12xy+30xz-20yz$

উদাহরণ ১৪। সরল কর: $(2x+3y{)}^2-2(2x+3y\left)\right(2x-5y)+(2x-5y{)}^2$

সমাধান:

ধরি, 2x + 3y = a এবং 2x - 5y = b

প্রদত্ত রাশি

$=a^2-2ab+b^2$

$=\left\{\right(2x+3y)-(2x-5y){\}}^2$

$=\{2x+3y-2x+5y{\}}^2$

$= {\left(8y\right)}^2$

$= 64y^2$

উদাহরণ ১৫। x = 7 এবং y = 6 হলে, $16x^2-40xy+25y^2$ এর মান নির্ণয় কর।

সমাধান: প্রদত্ত রাশি

$= 16x^2-40xy+25y^2$

$=(4x{)}^2-2\times 4x\times 5y+(5y{)}^2$

$={(4x-5y)}^2$

$={(4x7-5x6)}^2$

$= {(28-30)}^2$

$= {(-2)}^2$

$= (- 2)(- 2)$

= 4